無料のツールXcosを使って、一階微分方程式をシミュレーションする方法を紹介します。
はじめに
この記事では、無料のツールXcosを使って、一階微分方程式をシミュレーションする方法を紹介します。
微分方程式といっても「数学の勉強のため」だけではありません。
これをやっておくと、「制御工学」のとっかかりとして最適なんです。
いきなり制御理論に入るよりも、まずは準備体操として、気軽ににxcosでシミュレーションしてみてください。先に微分方程式に慣れておけば、数学への苦手意識によるハードルを大幅に下げられます。
この記事でやること
本記事では、以下の微分方程式を、Xcosでシミュレーションします。
この式は「ニュートンの冷却法則」と呼ばれていて、「物体の温度が変化する速さは、その物体と周囲の環境温度との差に比例する」という物理法則を表したものです。
(ちなみに、kは 冷めやすさを表す係数です。周囲の環境や物体の性質によって、その値が決まります。 )
例えば、熱いお茶を室内に置いたとき、部屋が寒ければ寒いほど、お茶は勢いよく冷えていきますよね。
こんな感じで当たり前レベルで把握している現象なので、計算結果が直感と一致しやすく、とっかかりにちょうどよい題材だと思います。

熱いお茶が冷める時間をざっくり探る・・・的な題材だと思って下さい。
▼ この記事のゴールとして、Xcosのシミュレーション結果のグラフを出し、解析解と比べるところまでやります。
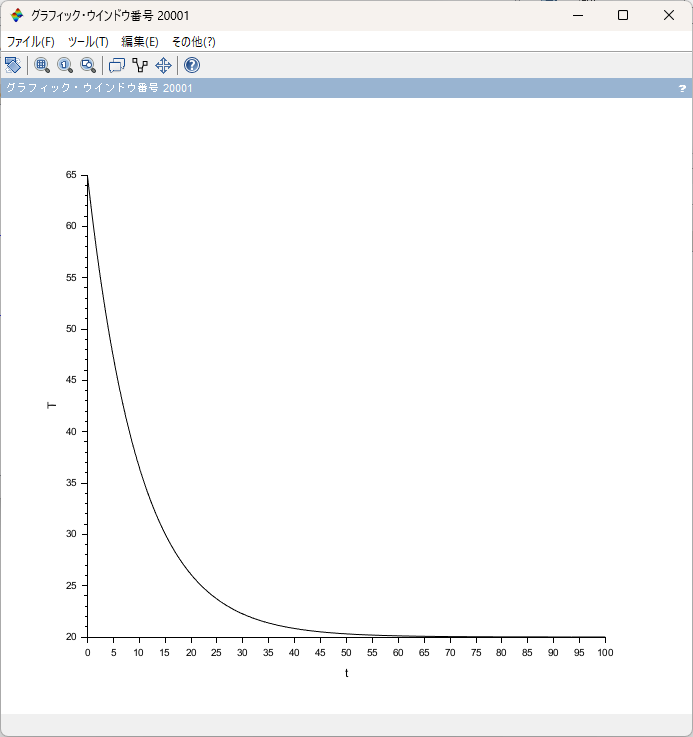
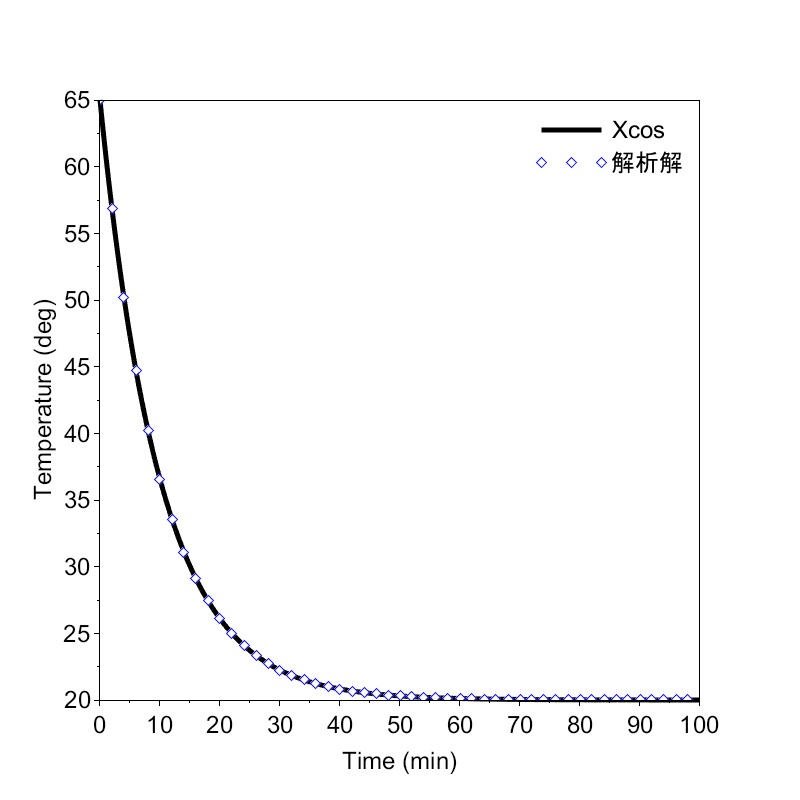
あくまで「とっかかり」なので、へ~この式からこんな波形ができるんだ~ぐらいの軽い感じでOKです。
Xcosを準備する
シミュレーションには、無料のXcosというソフトを使います。
Xcosは、オープンソースの数値計算ソフトウェア Scilab (https://www.scilab.org/) に付属するシミュレーションツールです。
▼ ダウンロードは、以下のリンクから可能です。ご自身の環境のOSを選択してください。
▼ インストールが済んだら、まずはScilabを立ち上げます。
▼ そして、メニューバーのアプリケーション→Xcosを選択すると、立ち上がります。
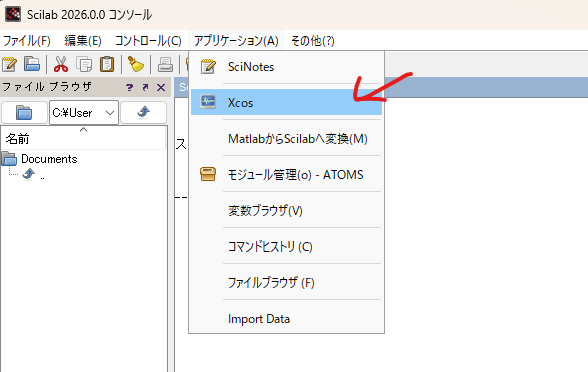
▼ Xcosが起動しました。下図赤枠内が、Xcosです。
基本的な使い方
操作はとてもシンプル。左のパレットブラウザから必要なブロックを選択し、右の作業ウィンドウ内にドラッグ&ドロップします。ブロック間をつなぐ線は、ブロックの三角形をドラッグします。
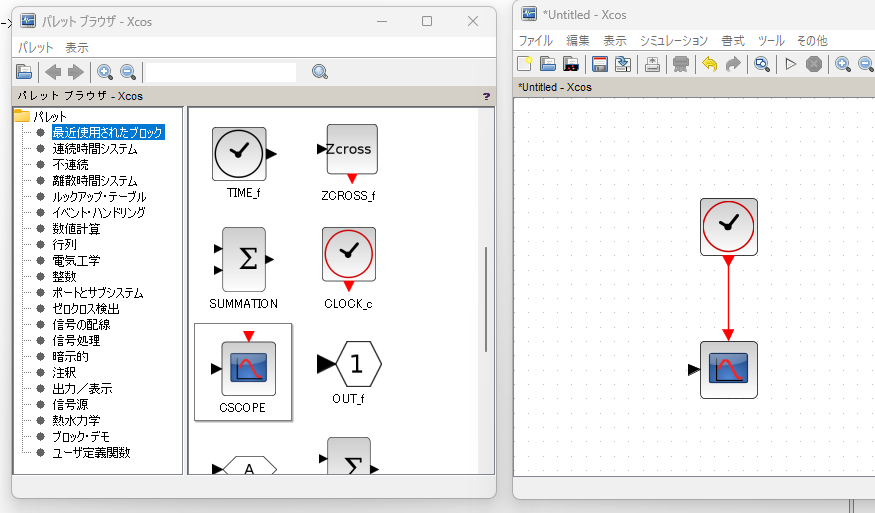
必要に応じて、式の変形
微分方程式をブロックで表現するため、最高階の導関数が左辺に単独で現れる形に変形します。
例えば、\( y” + 5y’ + 6y = 0 \) なら、\( y” = -5y’-6y \)という感じです。
Xcosでは、右辺の式を積分ブロックに入力し、それを順に積分することで、低い階数の導関数や元の変数を計算する構成にするためです。
さて今回は、冒頭で紹介の通り、以下の微分方程式をシミュレーションするというお話でした。
\[ \frac{ dT }{ dt }=-k(T-Ta) \]※ 式を見やすくするため、これ以降、時間微分の表記は次のように書きます。
\[ T’=-k(T-T_a) \]この場合、すでに最高階の導関数が左辺に単独で現れているので、特に変形せずこのまま式を使います。
仕上げとして、以下のように積分のかたちに直しておくと、後でブロックを配置する際にわかりやすいです。
▼「微分したら \( -k(T-T_a) \)になる関数」を求めたいので・・・
\[ T’=-k(T-T_a) \quad \Rightarrow \quad T=\int \{ -k(T-T_a) \} dt \]ブロックを配置する
ブロックを組んでいきます。先ほどの式を見ながら、まずはブロックを配置していきます。
- 諸条件
- k=0.1
- Ta=20℃(室温)
- T(0)=65℃(初期温度)
▼ 下図に、ブロックを配置した様子と、配置するブロック名を書いています。
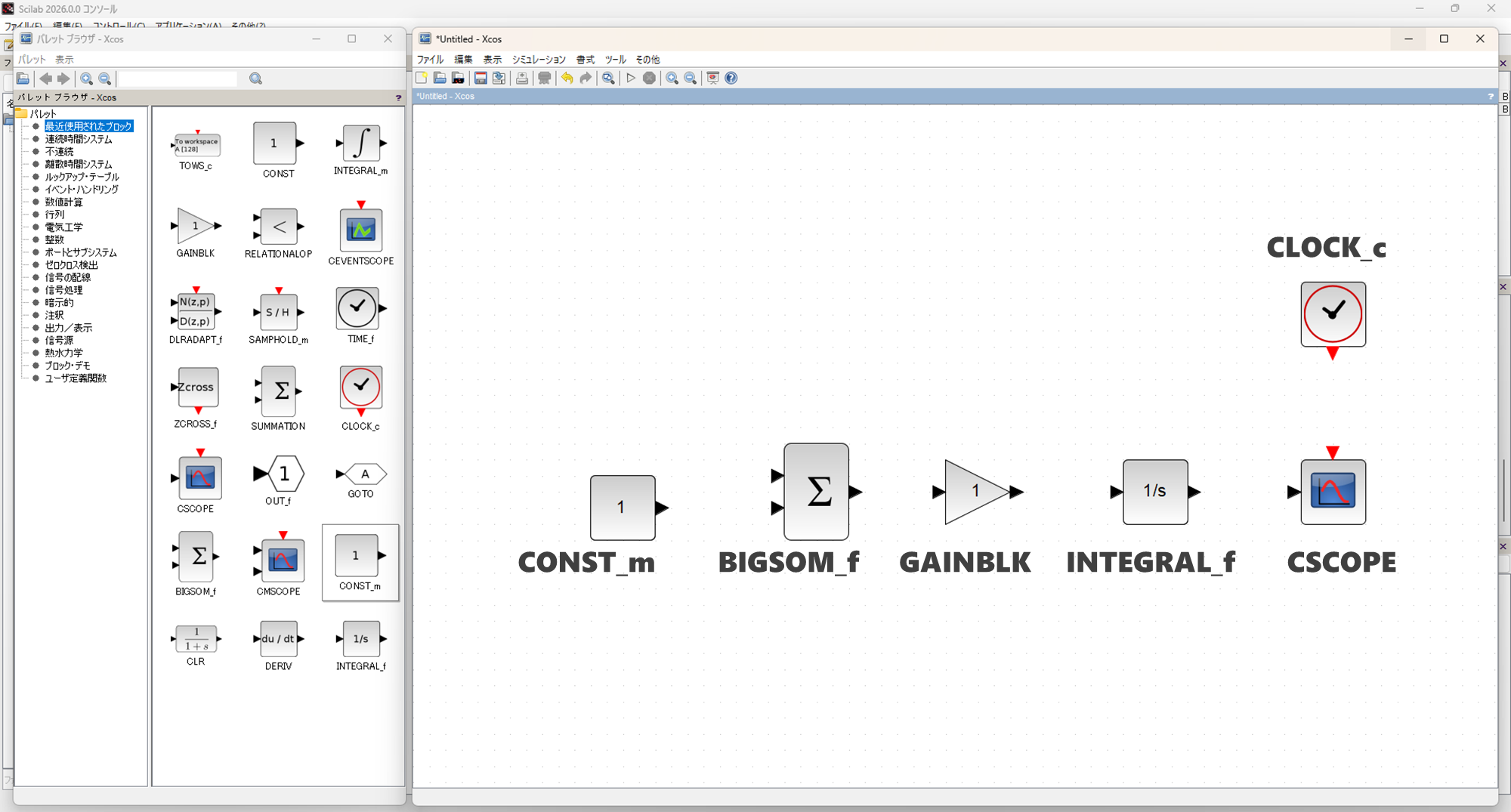
ブロックは、以下のものを配置しています。
| ブロック名 | 概要 | 用途 | 設定値 |
|---|---|---|---|
| CONST_m | 定数ブロック | 定数を定義する。 | 20 |
| BIGSOM_f | 加算・減算ブロック | 複数の信号を足し合わせたり、差し引いたりする。 | [1;-1] |
| GAINBLK | ゲインブロック | 入力信号に対して、設定した倍率を掛け合わせる。 | -0.1 |
| INTEGRAL_f | 積分ブロック | 入力された信号を時間で積分する。 | 65(Initial state) |
| CSCOPE | 波形表示ブロック | 計算結果をグラフとして表示 | 事項参照 |
| CLOCK_c | クロックブロック | 表示や計算を行う更新タイミングを制御する | 事項参照 |
ブロックのパラメーターを入力
各ブロックは、ダブルクリックするとパラーメーターを入力できます。
設定値は、前項を参照ください。
▼ 例えば、左側の定数ブロック(名前:CONST)をダブルクリックして、室温を入力します。
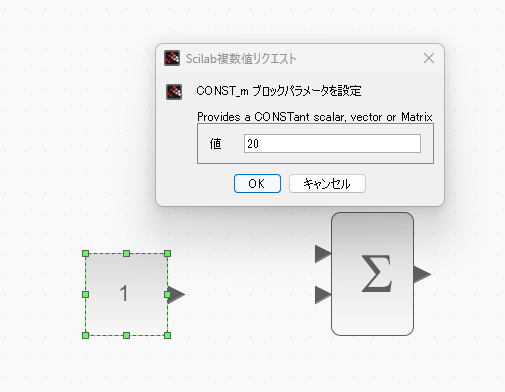
ブロックをつなぐ
▼ ブロック同士を、つなぎます。(対象同士をマウスでドラッグ)
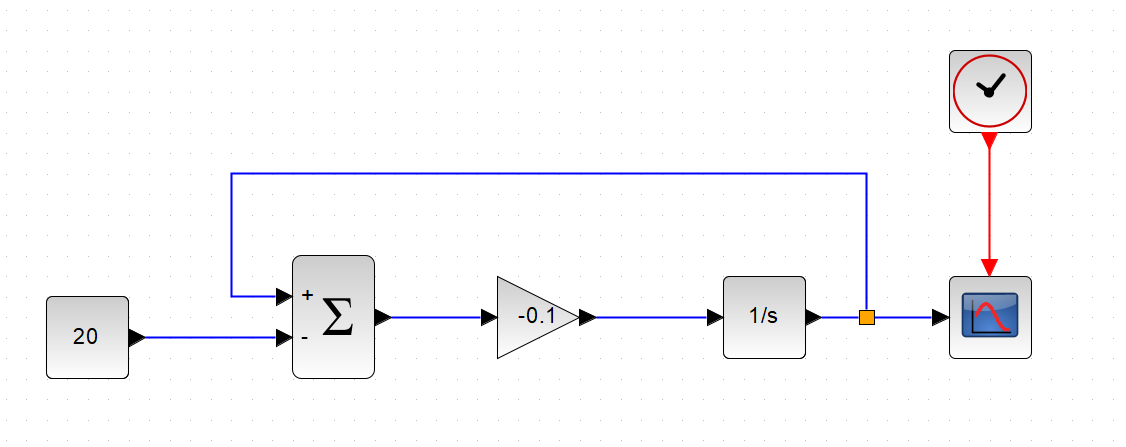
ブロックの細かい仕様は、以下のドキュメントをご覧ください。
諸々の設定をする
あとは、諸々の設定をしていきます。
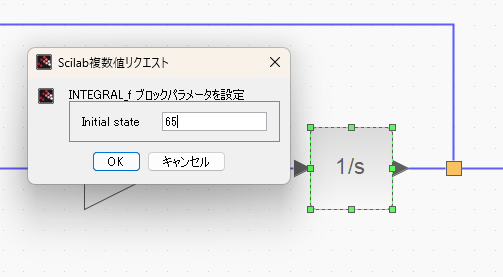
初期値を入力
INTEGRAL_fブロックに、初期条件を入れます。T(0)=65℃(お茶を入れた直後の温度)の想定なので、65と入力。
シミュレーション時間の設定をする
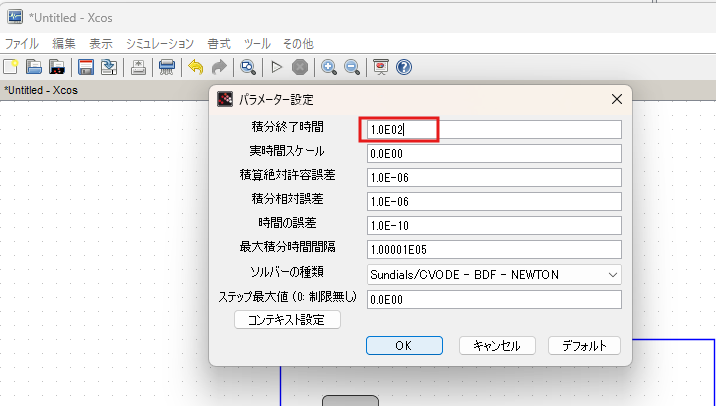
▼ 上部メニューバーの シミュレーション→ 設定 をクリック。
- 今回はt=100までの変化をみたいので、1.0E02(=100)と入力します。
グラフの表示設定をする
CLOCK_cと、CSCOPE。この2つのブロックを設定をして、グラフの見え方を調整します。
CLOCK_c 時計のアイコン
▼ 下図のようなかんじで。
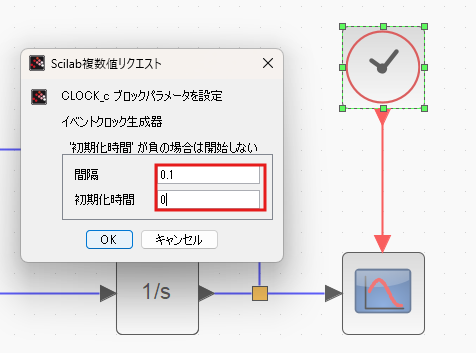
詳しい仕様:https://help.scilab.org/docs/2026.0.0/en_US/CLOCK_c.html
CSCOPE グラフのアイコン
▼ 下図のようなかんじで。特にRefresh Periodとバッファの大きさは、環境に合わせて変えておきます。
- グラフのt軸(横軸)の目盛りを100まで表示したいので、Refresh Periodは100
- バッファの大きさ:先ほど設定したclock_cの周期が0.1なので、100/0.1=1000と入力
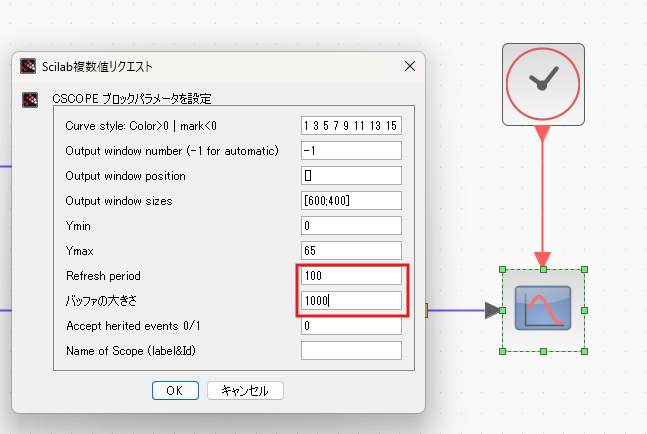
詳しい仕様:https://help.scilab.org/docs/2026.0.0/en_US/CSCOPE.html
シミュレーション実行
あとはもう、シミュレーションを実行するだけです。
メニューバー付近の三角形のアイコンをクリックすると、シミュレーションが開始されます。
別窓で、グラフが出てきました。
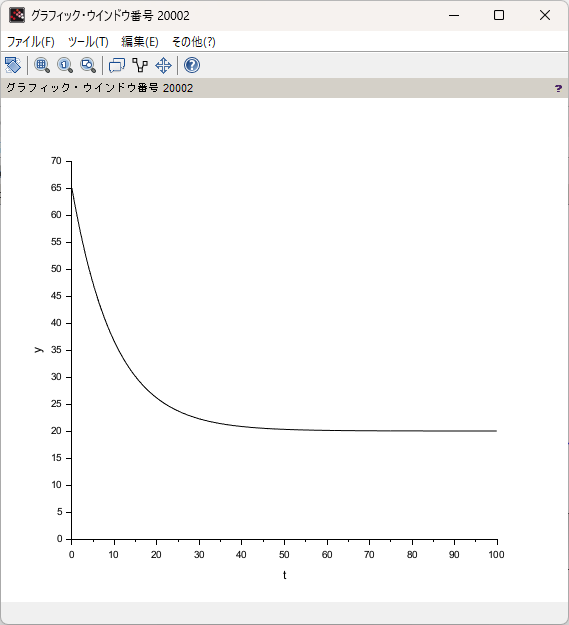
もし、一部分しか表示されていないなどの場合は、「内容に合わせてフレームを調整」で見えるようになります。
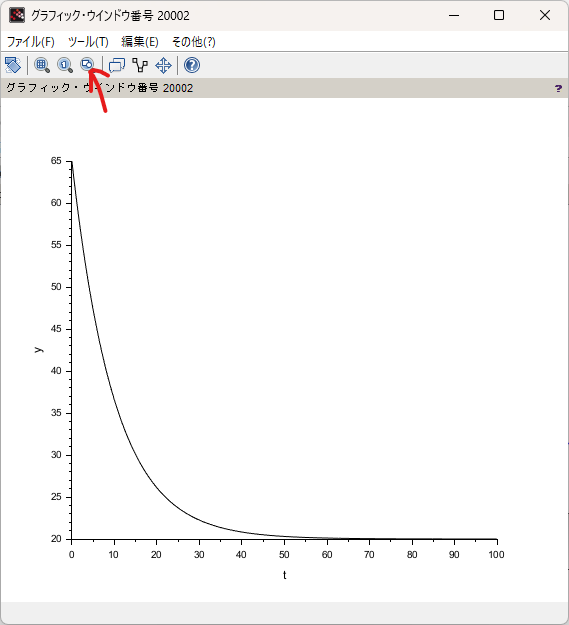
無事グラフを出力できたので、観察すると見たまんま、以下の情報が読めます。

- 指数関数になっているっぽい
- 65℃あったお茶が、だいたい55分以降は室温まで冷めて、以降は安定した。
基になった微分方程式と見比べると、普通に温度の冷め方を表していたんだな~ということがわかります。
手計算と比べると・・・?
さて、それっぽいグラフはできましたが、果たしてちゃんと出力されてるのか、判断できませんよね。
初めて触ったXCOSですから、もしかしたら設定が間違ったりして、変な結果が出てるかも……。
そこで、手計算と比べてみましょう。
解析解を出す
▼ グラフを描くため、解析解を出しました。
※ 変数分離法で解けます。微分方程式の参考書のたいてい一番初めに載ってるテクです。
\[ 変数分離を行いやすくするため、 T’の表記を戻すと..\\[ 15pt ] T’=-k(T-T_a) \quad \Rightarrow \quad \frac{ dT }{ dt }=-k(T-Ta) \\[ 15pt ] 公式通り積分して \\[ 5pt ] \log\lvert T-T_a \rvert = -kt+C (Cは積分定数) \\[ 15pt ] 指数関数の形にすると \\[ 5pt ] T−Ta=Ce^{-kt} \] \[ 初期条件T(0)を当てはめると \\[5pt ] T_0 = T_a + C \\[5pt ] Cが求まり… \\[5pt ] C=T_0-T_a \\[15pt ] 初期条件を満たす解がでました \\[5pt ] T(t) = T_a + (T_0-T_a) e^{-kt} \]プロットする
先ほど出した解析解を、Scilab(xcosの本体のソフト)でプロットし、XCOSの結果と重ねてみました。
青いダイヤのマークが、解析解の点です。ほぼ、Xcosと一致しています。Xcosの出力にミスはなさそうです。

▼ 元の式と、ブロックを再掲
\[ \frac{ dT }{ dt }=-k(T-Ta) \]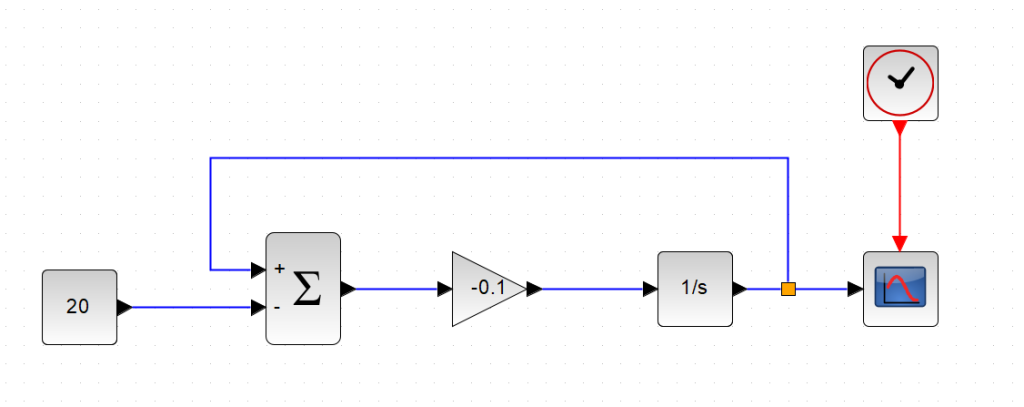
参考文献
- デヴィッド・バージェス、モリー・ボリー著、垣田高夫・大町比佐栄訳(1990)『微分方程式で数学モデルを作ろう』日本評論社
- Scilab (発行年不明)「Xcos for beginners tutorial」Scilab. https://www.scilab.org/xcos-for-beginners-tutorial, (閲覧日: 2026年1月27日)
オススメ本
私は初手で制御工学の本を読み撃沈したので、中断。まずは微分方程式の勉強から始めました。なかでも、以下の本がわかりやすかったので紹介します。
▲ 微分方程式の入門書です。
実例から数式の解説へと移る流れで「微分方程式が何に役立つのか」を理解できます。新書なので手軽に読み進められるため、最初の一冊として最適です。
実利を先に知ると学習意欲を維持しやすいです。いきなり解法のテクニックを学んでもなかなか頭に入らないので、まずは本書で活用のイメージを掴むことで、本格的な数学書へ進むための動機付けになります。
▲ 物理現象のモデル化に焦点をあてた、微分方程式のテキストです。
モデル化に特化しているので、解法自体の解説は詳しくありません。ただ第1章~2章で基本の微積分や変形分離などの解法の解説があるので、ほかの数学本で勉強したことがある人なら、軽く復習ができます。
本丸の3章からは、直接積分形、一階斉次形、一階非斉次形といった微分方程式の型ごとに、それぞれ対応する物理現象のモデルが紹介されています。
各モデルについて、式の仕組みや意味が丁寧に解説されているので、「モデル化されたこの式を解くと何が出てくるのか」が分かるようになります。
数学的な解法だけ勉強していると「結局何に役立つのか」が具体的に見えず、学習の興味が薄れてしまいがちですが、理論と現実のつながりを実感しながら読み進めることができます。
▲ 微分方程式の数学的な解法に特化した入門書です。
第一章で微分方程式の概要と微積分の復習から始まり、第二章からは一階微分方程式、線形微分方程式など、計算手順を中心に学ぶ構成になっています。
ちなみに、この記事でも使った変形分離法は、第二章の冒頭で丁寧に解説されています。
説明→例題→解説という流れなので、「ひたすら文章を読まされて疲れる」ということは、少ないと思いました。
本書全編をすぐに読み切る必要はなく、まずは第一章の微積分の復習と第二章の一階微分方程式の範囲を整理しておくだけでも、その後の学習がスムーズになります。
自力で検算ができると、シミュレーション結果の妥当性を判断するのに役立ちます。
さいごに
制御工学が「意味不明」で投げ出したことはありませんか?
私は本を開いても、いつも最序盤で挫折し、積読を増やすばかりでした。
制御工学では、制御対象の振る舞いを微分方程式でモデル化して表現します。ちなみに、今回の記事では、お茶の温度変化をモデル化していました。
私の場合、勉強スタート時は「そもそも、モデル化された微分方程式から意味不明」だったんですよね。そこでまずは微分方程式の把握から始めたら、少しずつ抵抗が薄れてきました。
いきなりラプラス変換や伝達関数に入る前に、Xcosで気軽にシミュレーションを試してみてください。無料ですし、パラメータを変えて結果を眺めてるだけでも、自然に慣れてきます。


























コメント